【数据结构】手写平衡二叉树(AVL)
【数据结构】手写平衡二叉树(AVL)

积千里跬步,汇万里江河。每天进步一点点,终有一天将成大佬
本文源代码:手写AVL树
什么是平衡二叉树?
平衡二叉树,又称为AVL树,当树不是空树时,它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。AVL树查找的时间复杂度为O(logN)。
平衡二叉树基本特点
- 左右子树深度差不能大于1
- 左边子树永远比根节点小
- 右边子树永远比根节点大
平衡二叉树基本结构及操作
- 左左结构——右旋
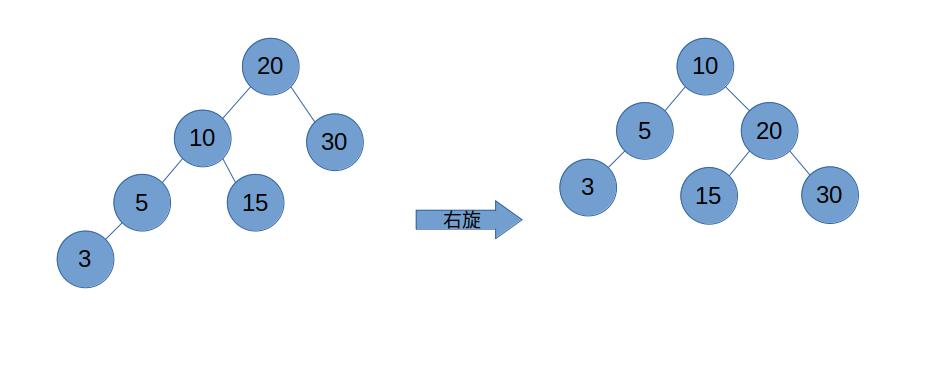
- 右右结构——左旋
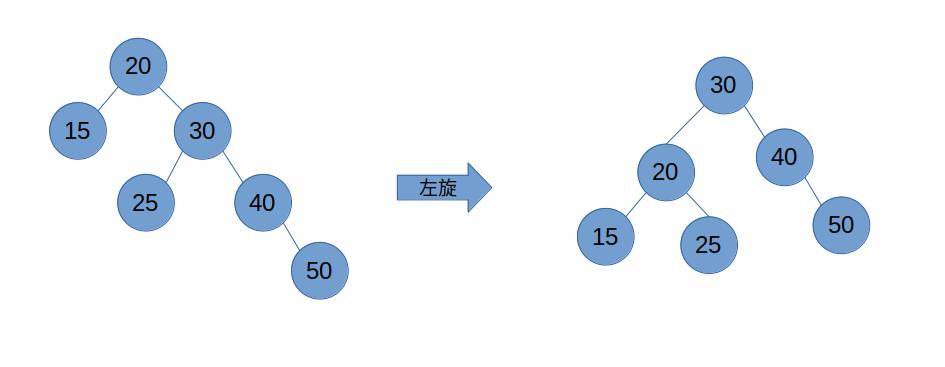
- 左右结构——左子先左旋,然后整体右旋
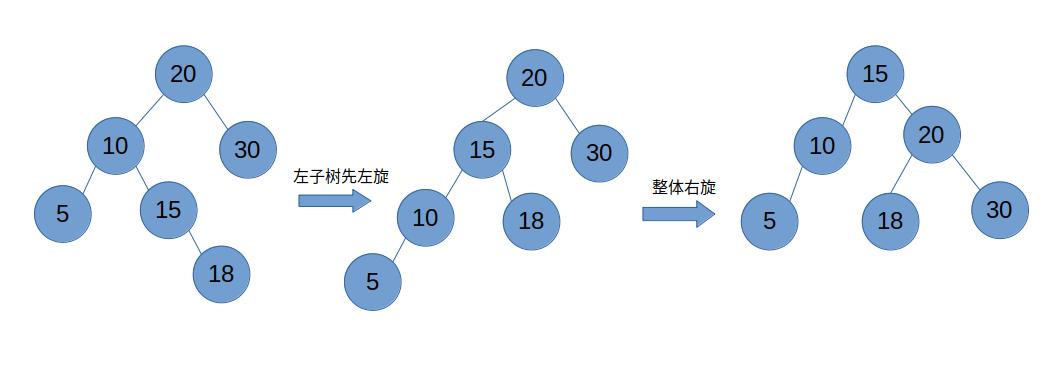
- 右左结构——右子先右旋,然后整体左旋
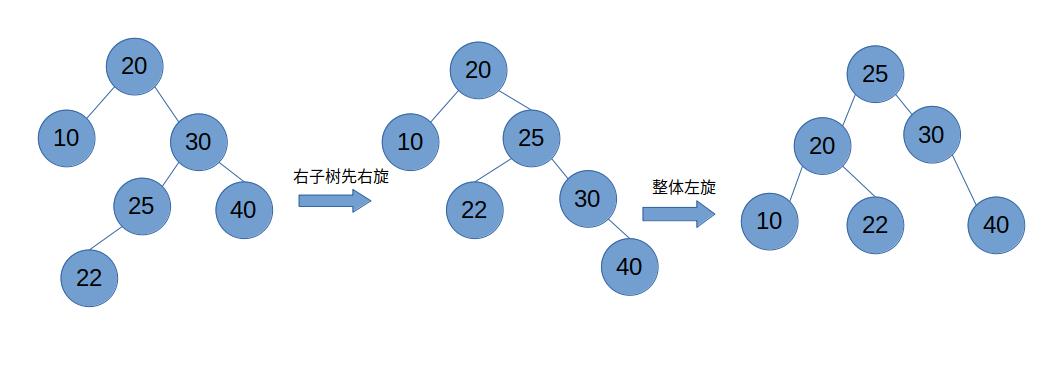
代码实现
先创建一个内部类Node,来表示树的每个节点
public class AVLTree {
private Node rootNode;
//二叉树节点
private class Node{
public Node parent; //父
public Node left; //左子树
public Node right; //右子树
@NotNull
public int data; //存放的数据
private int depth; //深度
private int balance; //平衡因子
//有参构造方法
public Node(int data){
this.data=data;
this.depth=1;
this.balance=0;
}
}
}
插入数据
暴露一个方法给外部调用
/**添加数据方法*/
public void add(int data){
if (this.rootNode==null){
this.rootNode=new Node(data);
}else {
this.insert(rootNode,data);
//判断根节点是否有父 有的话说明有旋转操作,更新根节点
if (this.rootNode.parent!=null){
this.rootNode=this.rootNode.parent;
}
}
}
实际内部是调用另一个insert方法:
private void insert(Node root,int data){
//插入的数据比根小
if (data<root.data){
if (root.left==null){
root.left=new Node(data);
root.left.parent=root;
}else {
this.insert(root.left,data);
}
}
//插入的数据比根大
if (data>root.data){
if (root.right==null) {
root.right=new Node(data);
root.right.parent=root;
}else{
this.insert(root.right,data);
}
}
root.balance=this.getBalance(root);
if (root.balance>1){
//判断左子的平衡因子
if (root.left.balance<0){
this.leftTurn(root.left);
}
this.rightTurn(root);
}
if (root.balance<-1){
//判断右子的平衡因子
if (root.right.balance>0){
this.rightTurn(root.right);
}
this.leftTurn(root);
}
root.depth=this.getDepth(root);
root.balance=this.getBalance(root);
}
右旋
右旋的操作如下
- 我父变成左子的父
- 左子变成我的父
- 我变成左子的右子
- 左子的右子变成我的左子
- (当左子的右子存在时)我变成左子的右子的父
- 计算左右节点的深度
- 计算深度差
private void rightTurn(@NotNull Node node){
Node parent=node.parent;
Node leftSon=node.left;
Node leftSon_rightSon=leftSon.right;
//如果父不为空,判断我是在父的左节点还是右节点
if (parent!=null){
if (node==parent.left){
//我在父的左节点上,把我的左子变成父的左子
parent.left=leftSon;
}
if (node==parent.right){
//我在父的右节点上,把我的左子变成父的右子
parent.right=leftSon;
}
}
leftSon.parent=parent;
node.parent=leftSon;
leftSon.right=node;
node.left=leftSon_rightSon;
//如果左子的右子确实存在的
if (leftSon_rightSon!=null){
//我变成左子的右子的父
leftSon_rightSon.parent=node;
}
//重新计算深度和平衡因子
node.depth=this.getDepth(node);
node.balance=this.getBalance(node);
leftSon.depth=this.getDepth(leftSon);
leftSon.balance=this.getBalance(leftSon);
}
左旋
左旋的操作如下
- 我的父变右子的父
- 右子变成我的父
- 我变成右子的左子
- 右子的左子变成我的右子
- (当右子的左子存在时)我变成右子的左子的父
- 计算左右节点的深度
- 计算深度差
private void leftTurn(@NotNull Node node){
Node parent=node.parent;
Node rightSon=node.right;
Node rightSon_leftSon=rightSon.left;
if (parent!=null){
if (node==parent.left){
parent.left=rightSon;
}
if (node==parent.right){
parent.right=rightSon;
}
}
rightSon.parent=parent;
node.parent=rightSon;
rightSon.left=node;
node.right=rightSon_leftSon;
if (rightSon_leftSon!=null){
rightSon_leftSon.parent=node;
}
node.depth=this.getDepth(node);
node.balance=this.getBalance(node);
rightSon.depth=this.getDepth(rightSon);
rightSon.balance=this.getBalance(rightSon);
}
计算深度
/**计算深度*/
private int getDepth(Node node){
int depth = 0;
if(node.left==null && node.right!=null) {
depth=node.right.depth;
}
if(node.right==null && node.left!=null) {
depth=node.left.depth;
}
if (node.right!=null && node.left!=null) {
depth=Math.max(node.left.depth,node.right.depth);
}
depth++;
return depth;
}
计算平衡因子
/**计算左右深度差*/
private int getBalance(Node node){
int leftDepth = 0;
int rightDepth = 0;
if(node.left!=null){
leftDepth=node.left.depth;
}
if(node.right!=null){
rightDepth=node.right.depth;
}
/**
* 左减右
* 为负数:右边子树高
* 为正数: 左边子树高
* */
return leftDepth-rightDepth;
}
附言
如果代码和静态图看不太明白的话,这边推荐几个动画演示的网站(可能需要科学上网):